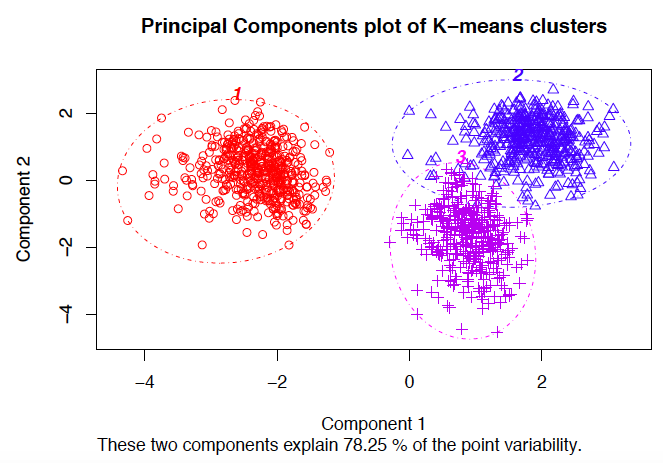
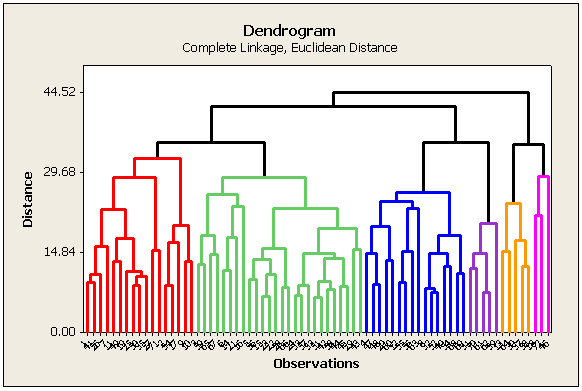
Análise de Equações Estruturais: abordagem de análise
A Análise de Equações Estruturais (AEE) é uma extensão dos modelos lineares generalizados – Generalized Linear Models (GLM) – que permite ao investigador testar simultaneamente um conjunto de equações de regressão. Os softwares utilizados (SPSS AMOS ou LISREL, por exemplo) permitem testar desde os modelos mais simples (como os modelos de regressão, Anova e Ancova) até à análise das relações entre as varáveis de modelos mais complexos, como a análise factorial confirmatória e análises de séries temporais.
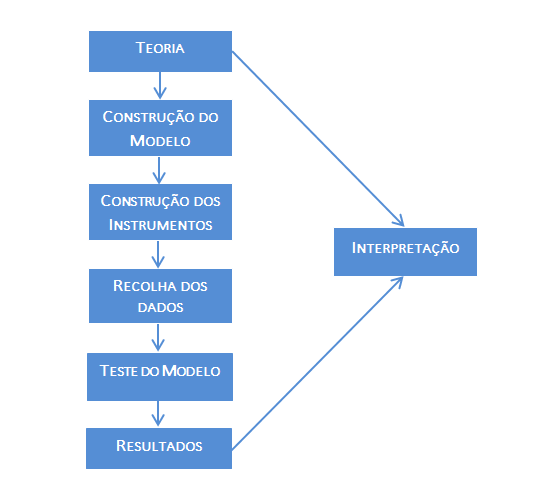
O diagrama seguinte ilustra a abordagem de base para a realização de uma análise de equações estruturais:

A abordagem básica para a realização de uma análise de equações estruturais assenta numa teoria, a partir da qual construímos o modelo a testar. Atendendo ao tipo de variáveis ou fatores envolvidos na teoria, construímos os instrumentos a utilizar na recolha dos dados empíricos. O software de análise estatística ajusta os dados ao modelo especificado e produz os resultados (que incluem as estatísticas gerais de ajustamento do modelo e as estimativas dos parâmetros).
Os inputs para a análise de equações estruturais são geralmente uma matriz de covariância de variáveis, medidas como scores, embora às vezes também se recorra às matrizes de correlações ou às matrizes de covariâncias e médias. O investigador fornece os dados em bruto, enquanto o analista converte estes dados em covariâncias e médias para proceder à análise.
O modelo consiste num conjunto de relações entre as variáveis medidas. Estas relações são então expressas como restrições sobre o conjunto total das relações possíveis.

Os resultados apresentam os índices de ajustamento do modelo, as estimativas dos parâmetros, os erros padrão e as estatísticas de teste para cada parâmetro livre no modelo.
Por fim, confrontamos os resultados obtidos com a teoria (ou a literatura) e nesta interpretação vamos confirmar, ou rejeitar, as hipóteses subjacentes ao modelo, analisar as relações entre as variáveis e avaliar a bondade de ajustamento do modelo proposto com base nos índices da bondade de ajustamento.